対話式算数第44話：素因数分解

対話式算数：各回の概要

今回は数の性質の応用問題を解くときに大活躍する素因数分解を学習します。

「数の性質を利用する」というと、偶数・奇数に注目するか、素因数分解をして構造を理解して利用するかが主な考え方です。

興味のある方はこちらにどうぞ

対話式算数とは

小４対話式算数

1. 第44話：素因数分解

第44話：素因数分解

44・1

素数という単語を見てもピンとこないので、合成数を説明し、素数の意味に迫りました。

素数を書き出すときは、一の位が5ではない奇数を書き出してから消した方が良いとしています。

44・2

素因数分解という単語を見てもピンとこないので、因数分解の話題を出し、素因数分解の意味に迫りました。

44・3

平方数をつくる問題は、見やすく、読みやすく説明できていると思います。

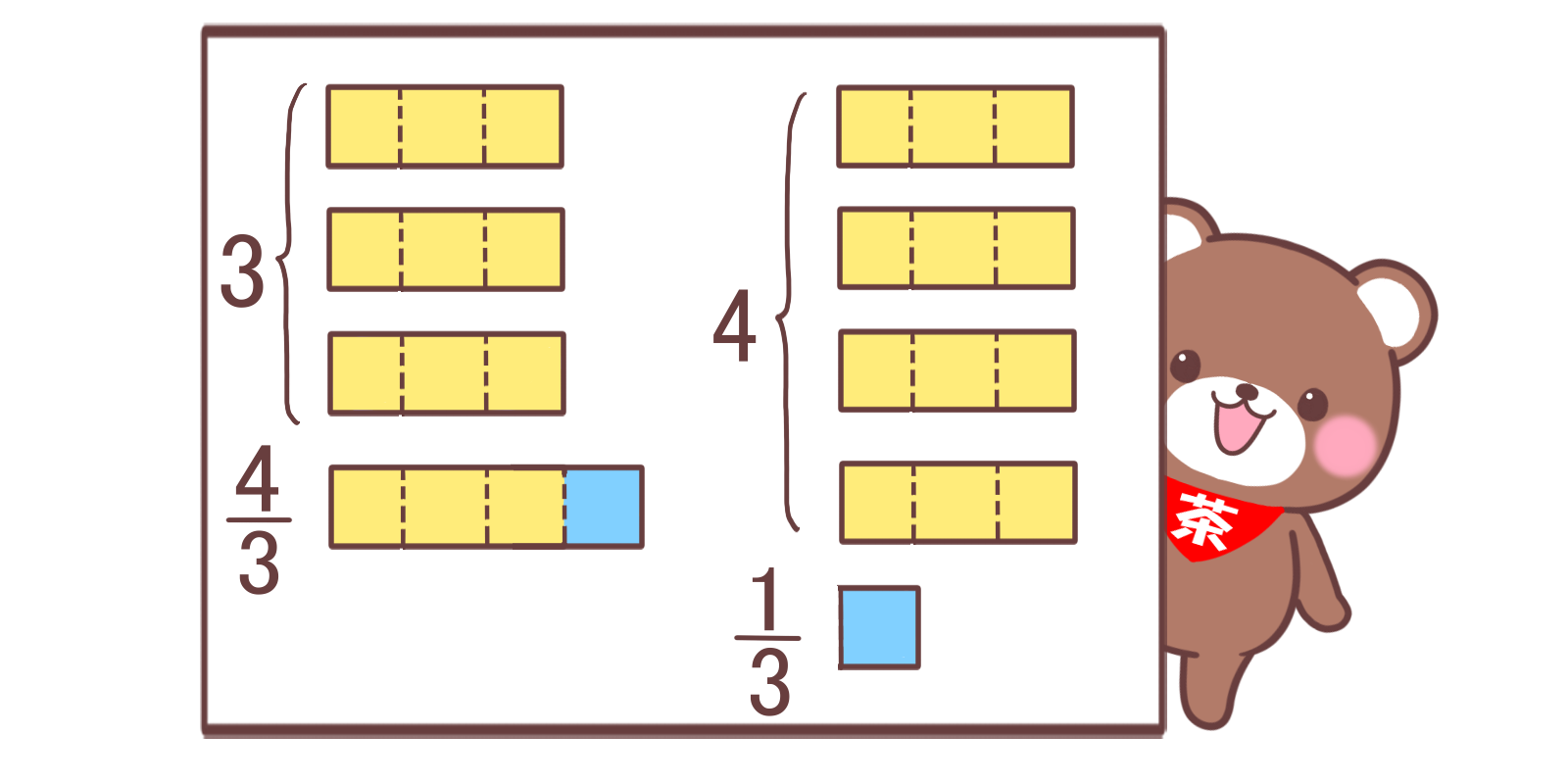
分数バージョンも分かりやすく説明できていると思います。

44・4

既約分数を数える問題は、今回はベン図ではなく、周期性を利用してみました。

楽な方を選んで使えると良いと思います。

44・5

割れる回数は、高度ですが、高度な割には解ける子が多い印象です。

最初は分数で地道に考えると良いと思います。

かなりのページ数をさいて説明しています。

10で割る回数は、導入でハンバーグを例えにしています。

練習問題

番号	難	要	講評
1	A		1～50までの奇数を書いて、素数以外を消しましょう。
2	A		200以上の奇数を1つ1つ確認します。
3	B	サ	大変ですが、51～100までの奇数を書いて、素数以外を消しましょう。
4	Ａ		2、3、5、7、……の素数で割れるか試しましょう。19くらいまで試すようにします。
5	Ｃ	ヒ	素因数分解で解いて欲しいのですが、「大きさの検討」「一の位の注目」でも解けます。大きさを検討していれば、素因数分解で11と13があった時点で143だと気づくと思います。
6	Ｃ	サ	地道な書き出しです。小さい順から書き出しましょう。
7	Ｂ	ゼ	504を素因数分解して、足りないものを補充するという感覚です。
8	Ｂ	ゼ	分母の84を素因数分解して、足りないものを補充しますが、そのときに、公平に分子にも補充します。
9	Ｂ	ゼ	Bが3つありますが、仕組みは8番と同じです。補充する意識で解きましょう。
10	Ｃ	ゼ	45を素因数分解して、3の倍数または5の倍数と分かったら、ベン図か周期性で解きます。５年生以降は周期性がいいです。
11	Ｃ	ゼ	90を素因数分解すると2と3と5が出てくるので、ベン図は少々厳しいです。周期性で1～30を調べる（その半分の15まで）と良いと思います。
12	D	ヒ	約数の個数に関連する考え方で解きます。4年生には難しい問題です。
13	B	ゼ	分数の模式図をかいて、約分するイメージで解くことをお勧めします。
14	B	ゼ	5で割れる回数になります。13番と同様に、分数の模式図をかいて、約分するイメージで解くことをお勧めします。
15	Ｂ	テ	78＝2×3×13なので、13があれば！と考えます。