対話式算数第80話：円すいと角すい1

対話式算数：各回の概要

円すいや角すいの錐体は、小学生の指導要領から抜けていますが、中学入試では、問題文にサラッと「円すいの体積は、底面積×高さ÷3です」と載せて、堂々と出題しています。

それが良いことか悪いことかは分かりませんが、中学入試の範囲内の分野ということです。

興味のある方はこちらにどうぞ

対話式算数とは

小５対話式算数

1. 第80話：円すいと角すい①の概要

第80話：円すいと角すい①の概要

80・1

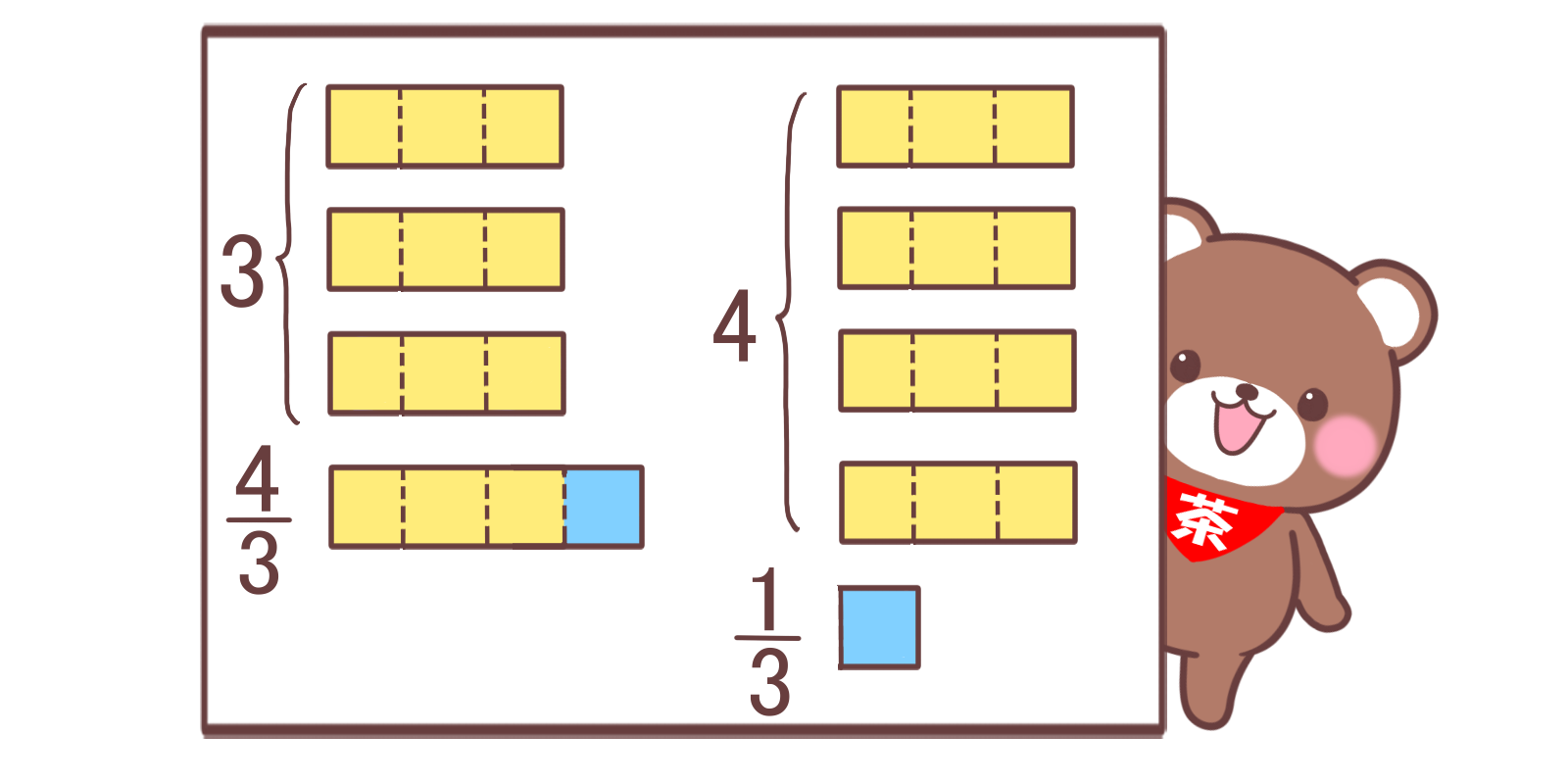
円すいの体積の公式の説明をしています。

円すいだと高度すぎて理解ができないので、三角すいと四角すいの体積の求め方の説明にしました。

公式は理解したものを使うということが原則だと思っていますが、この公式は、例外的に、理解する必要は無いと思います。

80・2

円すいの表面積です。

展開図で求めることを理解したら、解くときは、母線×底面の半径×3.14を使うようにしましょう。

80・3

角すいの辺と頂点と面の数の関係を学びます。

五角すいあたりをかいて、仕組みを見抜けば良いので、覚える必要はありません。

80・4

直方体のかどを切って三角すいを作る場合、三角すいの4面のうち、3面が直角三角形になります。

その三角すいは、3辺をかけて6で割る習慣を付けた方が良いです。

80・5

投影図です。

図を見て予測するのではなく、自分の知っている形の中のどれかを考えるようにします。

練習問題

番号	難	要	講評
1	Ａ		公式通りに体積を求めます。
2	A		円すいと円柱の体積を求めます。計算はスマートにやりましょう。
3	A		円すい2個と円柱の体積を求めます。計算はスマートにやりましょう。
4	Ａ		側面積と底面積を求めます。計算はスマートにやりましょう。
5	Ｂ	ゼ	円すいの側面積と円柱の側面積と円柱の底面積を求めます。
6	C	ヒ	外側の側面と、内側の側面と、下の底面の面積を求めます。2つの側面積は、それぞれ与えられた直角三角形の3辺の比で、母線を求めます。
7	Ａ		五角すいで仕組みを見抜くと良いと思います。
8	Ａ		例えば、五角すいの辺は10本です。2倍ですね。
9	Ｂ	テ	例えば、五角すいの頂点は6個で、辺の数は10本なので、合計16で、5×3＋1になります。
10	Ｂ	テ	㋐の体積を求めます。逆算で㋑の高さを求めます。
11	B	ゼ	合同な四角すい2つに分けます。四角すい1つを求めて2倍します。真上から見ると底面積が分かります。真正面から見ると高さが分かります。
12	B	ヒ	円すいの4分の1から三角すいをひいたら、体積が求められます。少々分かりにくいと思います。
13	B	ゼ	体積は、底面積も高さも分かるので、公式通りに求められます。表面積は、側面の三角形の高さが13㎝になることを納得してください。
14	Ｃ	テ	まず見取り図をかいてみましょう。円すいの側面、円柱の側面、円すい台の側面、円すい台の底面を求めます。上の円すいの側面と、下の円すい台の側面はくっつけることが計算を楽にするポイントです。
15	C	テ	軽く見取り図をかいてみましょう。長方形の側面3つと、曲面の側面1つと、底面2つからできています。