対話式算数第13話：角度２

対話式算数：各回の概要

小４対話式算数は4話ごと（1か月ごと）に分野が変わっていきます。

今週から平面図形に戻ります。

第1話の角度①よりもグッと難しくなります。

興味のある方はこちらにどうぞ

対話式算数とは

小４対話式算数

1. 第13話：角度②の概要

第13話：角度②の概要

13・1

三角定規の角度です。

30度・60度・90度・45度を使えば解ける問題から、戦略を練って解く問題まで幅広く載せています。

戦略はかなり細かく伝えています。

角度を書き入れすぎないことも大切です。

13・2

正方形と正三角形を組み合わせた図形は、ほぼ100％と言っていいほど二等辺三角形が出てきます。

そういう目で探すことが大切です。

13・3

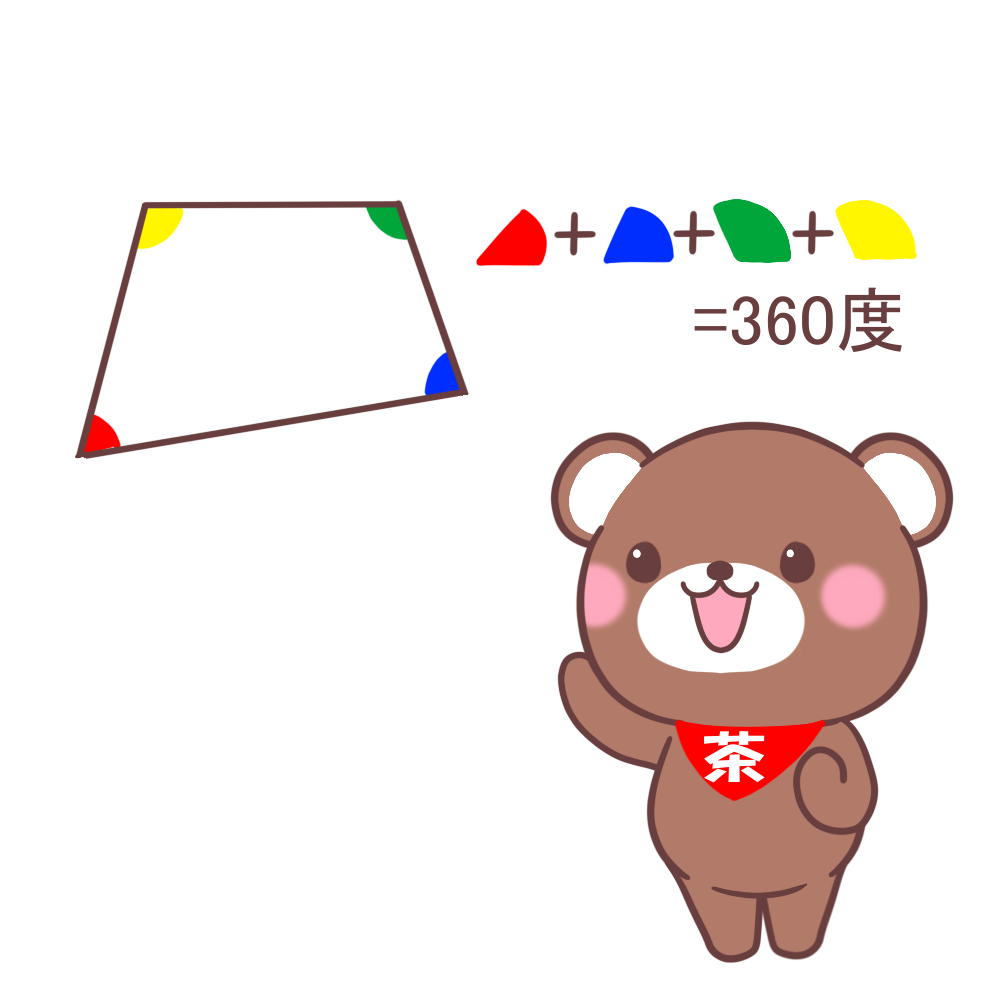
四角形の内角の和が360度を利用する問題です。

内部に三角形が2つ入っているからという理由で説明しています。

今回の5つのテーマの中では最も簡単だと思います。

とは言いましても、例題は単純な四角形ではなく、補助線をひいて四角形を作るタイプです。

今回の画像はここで載っているものです。

13・4

平行四辺形は向かい合う角度が等しく、隣の角の和が180度になることを、同位角と錯角で伝えています。

説明はそれほど詳しくは書いていませんが、カラーを使っているので分かりやすくなっていると思います。

四角形のグレードの話も入れています。

グレードがきちんと理解できていると、今回の範囲外ですが正方形の面積をひし形の公式で求めるときに違和感なく求められます。

例題は3つの解法で解いています。

このように角度は別解の宝庫ですので、4年生は角度をいろいろな解き方で解けるようにしていく学習が望ましいと思います。

13・5

図形を折り返す問題です。

例題は4つも入れています。

1つ目の例題は折り返す前の図形と折り返した後の図形は合同なので、角度が等しいことを利用する問題です。

2つ目の例題は重なる図形は二等辺三角形になりやすいことを伝える問題です。

3つ目の例題は折り返した図形の中には相似ができやすいことを伝える問題です。

相似は5年生で学習しますが、「形は同じで、大きさが違う図形」と軽く説明しています。

4つ目の例題は正方形を折り返すと二等辺三角形ができることを伝える問題です。

練習問題

番号	難	要	講評
1	A		三角定規の角度を書き入れましょう。
2	B	ゼ	2つの三角形の角度を書き入れていきます。
3	B	テ	三角形6個のうち、必要な3個の三角形を選び、その角度を書き入れていきます。三角形の外角の定理も利用すると良いでしょう。
4	B	ゼ	二等辺三角形と正三角形から、問題の条件に書いていない二等辺三角形を探して利用します。
5	B	ゼ	二等辺三角形（直角二等辺三角形）があることを見抜きます。
6	B	ゼ	150度の二等辺三角形があります。この形はよく出ますので慣れておきましょう。
7	A		四角形の内角の和の360度を使って解く問題です。右上の四角形で考えると良いと思います。
8	A		二等辺三角形を利用して、四角形ACDEの内角を考えるか、全体の四角形ABDEを考えます。
9	B	テ	例題と同じように補助線をひいて四角形をつくります。
10	B	ゼ	2つの平行四辺形の角度をすべて書き込んでみると、解き方が分かると思います。
11	B	テ	角Dが分かる→角ABCも角Dと同じと考えていくと、解けると思います。
12	C	テ	平行四辺形ABCDの4つの角が分かり、三角形CDEが二等辺三角形になることが分かると、解けます。
13	B	テ	㋐はCと同じです。32度を上手く使えば㋑を求められます。
14	B	ゼ	二等辺三角形があることを見抜きましょう。同位角や錯角という言葉で説明できるようにしましょう。
15	C	ゼ	三角形ABDが二等辺三角形なので、すべての角度が分かります。