- 2021年6月18日
このブログではお役に立ちたいを最重要テーマにしていますが、
私自身、本来は算数論を語る方が得意です。
ということで、ひさしぶりに算数について語っていきます。
受験算数をあまり知らない方は、一部、目を背けたくなる話になると思います。
タイトル通り、まず開成中の問題です。
2011年入試なので、かれこれ5年前です。
西山動物園では、開門前に長い行列ができていて、さらに、一定の割合で入園希望者が行列に加わっていきます。
開門と同時に、券売機を5台使うと20分で行列がなくなり、開門と同時に、券売機を6台使うと15分で行列がなくなります。
また、もし開門のときの行列の人数が50人少なかったとすると、開門と同時に券売機を7台使うと10分で行列がなくなります。
開門前の行列に並んでいる人数はいつも同じものとして、次の問に答えなさい。
(1)開門のとき、行列の人数は何人ですか。
(2)開門と同時に、券売機を10台使うと、何分で行列がなくなりますか。
私は2011年当時はまだ塾講師で、その年は女子クラスを担当していたので、開成の問題まで気が回っていませんでした。
当日発表校の合否の連絡を受け、対応し、翌日に備え、補講などに奔走していました。
同僚に、開成中の入試問題がネットで話題になっているよと教えてもらい、そういう目で初めてこの問題を見ました。
どうして話題になっているかすぐに分かりました。
普通に解いていくと、
行列が300人で、1分で10人やってきて、券売機1台で1分で5人さばけることが分かります。
(1)の答えが300人で、
(2)は券売機を10台にするので、1分で50人さばけるので、1分で50-10=40人減るので、300÷40=7.5分で行列はなくなります。
答えは7.5分となるのですが、これではほとんど典型題です。
さすがに開成ではこれはないと思うわけです。
どこに何が書いているわけではありませんが、開成中の出題者はこんなことを求めているわけではないと思います。
どの教科も、難関校になればなるほど、出題者との対話というか心理を読む必要があります。
深く考えすぎないこと、浅く考えないこと、ちょうどその学校で求められている読み取りをすることが大切です。
それ本当?と思われる方がいると思いますが、本当です。
算数はファジーの世界です。
では、典型題過ぎて気持ちが悪いので、開成の問題を再度考え直します。
1分で10人やってくるというのは、6秒で1人やってくることです。
券売機1台は1分で5人さばくので、12秒で1人さばくことができます。
券売機が10台になっても12秒で10人になるわけで、6秒で5台とはなりません。
すると、12秒で8人減るので、300÷8=37あまり4
12×37=444秒の時点であと4人残るので、その4人は当然12秒後にいなくなります。
444+12=456秒=7分36秒=7.6分となります。
さて、どちらが答えでしょうか?
これはあきらかに後者でしょう。
前者の7.5分のときは、開成でこれ?と疑問符が付きましたが、
後者の7.6分のときは、出題者はこれを求めていたんだ!と納得しながら解くことができました。
6秒で1人とか12秒で1人というように整数になり、しっくりきて、そう確信しました。
この納得感というセンサーが難関校合格には欠かせないのです。
とは言っても実際の採点ではどうなったか分かりません。
ザッと数枚の答案を見て、初志貫徹ではなく、配点、模範解答を代えてしまう場合もあるかもしれません。
7.6で正解、7.5で半分の得点というように総合的に判断したかもしれません。
あくまでも選抜テストですので。
次は芝中の問題です。
これは22年前の問題です。
1辺が1㎝の立方体の積み木で,ある立体をつくりました。図はその立体を正面,真横,真上から見た図です。
立体に使われた積み木は最も少ない場合で何個ですか。
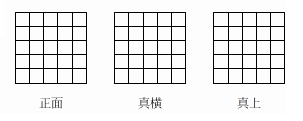
これを単純に考えると、
下の段は25個の立方体を敷き詰めて、対角線の1列だけ5段まで積めばいいので、
25+4×5=45個でできます。
しかし、算数の場合は、何もかいていないときは色の概念などはないので、
積み木と床の色の区別がありません。
すると、いま見えているのは立方体ではなくて床かも?
そう考えると、5ヶ所隙間をつくれます。
45-5=40個になります。
さて、答えはどちらでしょうか?
これは答えは45かもしれません。
あくまでも納得感をもとにです。
まず、芝中の出題者がどちらを想定して出題したかがポイントです。
受験生はそれと同調していることが大切です。
出題者が、受験生を読み切れずに、解答が代わる場合もあります。
40を想定していて、受験生は45が多ければ、45が正解になるでしょう。
45を想定していて、受験生は40が多ければ、両方正解になると思います。
45を想定しているときに、40が少数であれば、不正解ということになるかもしれません。
出題者の想定していた模範解答、そして受験生の解答
これが絡み合って採点は進められると思います。
ときどき、季節外れの時期に、採点ミスによる繰り上げ合格がありますが、
こういったことも原因の1つだと思います。
そろそろまとめに入ります。
受験生は、その学校の出題者と対話できる力をつけることが重要です。
違和感を感じる力、納得感を持って解き進めていく習性
こういった力が必要です。
そのためには、6年生の秋には受験校の出題難易度と同等の問題を豊富に練習することに尽きます。
そして、典型題ではその力はつきません。
解法を身につけておいて再生するだけですので。
捻りのある問題をしっかり練習することが大切です。
この6、7、8月に典型題をしっかり固め、早めの第一志望校の入試演習突入を理想の形としてがんばってください。







