「中学への算数」との速さの解説の比較

現在、スカイプ指導で東京出版の「中学への算数」を使用していますが、ときには、良い問題は、算数教材塾・探求の教材にも入れています。

題材は入試問題で、私の編集している教材に１問単位で組み込むだけですし、問題も解説も自らPCで文字をうって、図も描いていますので、著作権は全く問題ないと思っています。

せっかくですので、解説の比較をお目にかけたいと思いまして、ブログを書くことにしました。

単元は「速さと比」です。

中学への算数はダイヤグラムが大好きですが、私は、特定問題以外はダイヤグラムはかかない方針です。

特定問題とは

• 速さを変える回数が多い
• 向きを変える回数が多い
• 休むときがある

この３条件のうち１つ当てはまったらダイヤグラムを有力候補とし、２つ当てはまったら間違いなくダイヤグラムを描くという決め方です。

ダイヤグラムで解きやすい問題もあり、そういうのはいいですが、平面図形と比の技法を使って解くくらいならば、ダイヤグラムはかかない方がましだと思っています。

砂時計型の相似くらいなら好んで使いますが、中学への算数の速さの月の解説を見ていると、嗜好が合わないなと思ってしまいます。

では、問題です。

兄は走って、弟は自転車でA町から6km離れたB町に向かって同時に出発しました。兄と弟の速さの比は2：3で、弟はB町で用事を5分で済ませ、来た道と同じ道を通ってA町に戻ったところ、3分後に兄とすれちがいました。兄と弟は一定の速さで走っているものとすると、弟の速さは毎分何ｍですか。

2014年芝中2次の問題です。

芝中らしい良質の問題で、難度はそれほど高くはありませんが、身につけて欲しい要素があるので教材に入れようと思いました。

まずは中学への算数の解説です。

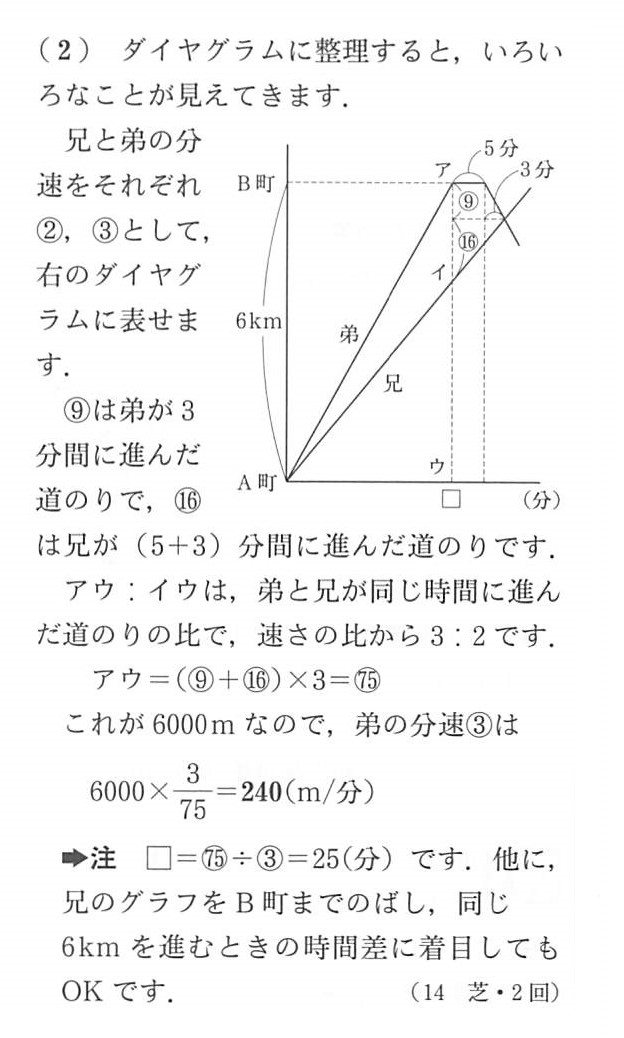
やはり、ダイヤグラムでした。

次は、算数教材塾・探求の解説です。

解き方はほぼ同じです。

最後の処理のところが異なりますが、そこでの優位性はないと思います。

ダイヤグラムを中心とした中学への算数の解説が良いか、算数教材塾･探求の解説が良いかという好みの問題です。

長距離移動で、新幹線が好きか、飛行機が好きかというくらいの差です。

問題点は、塾で好きじゃない解き方を教わり、速さを苦手にしている生徒さんが多いことです。

スカイプ指導で、速さが苦手な子に、私の解き方を教えると、すぐに吸収してできるようになります。

私の解き方が優れていると言っているわけではなく、いま苦戦しているなら、相性が悪いと判断した方が良いという意見です。

上の2つを見くらべても、最後以外は同じ解き方ですが、印象がかなり異なるという感想の方もいらっしゃると思います。

こっちでは身につかないけど、あっちなら身につくというような好き嫌いがある子も多いと思います。

速さは入試においては特に重要です。

苦手な状態で入試に挑むなんてことは、武器を持たずにクマを追い払おうとするようなものです。

お通いの塾の担当講師の解法が良いと思われています方は、慣れたのかもしれませんし、運が良かったのかもしれません。

そのままの勢いで取り組んで良いと思います。

中学への算数の解法が良いと思われた方は、購読をお勧めします。

もしも算数教材塾・探求の解き方が良いから、その解法を身につけたいと思われましたら、算数教材塾・探求の速さの教材をご購入いただくか、スカイプ指導で速さ一点主義で指導を受けるかのどちらかをご提案いたします。

速さは、場合の数と並び、問題を見て、どういう解き方をすれば良いか判断が迷う単元です。

しかし、場合の数よりも糸口の探し方はマニュアル化しやすいです。

先ほどのダイヤグラムのように、具体的に「こういう場合はこれ」という作戦の立て方があります。

入試で速さでアドバンテージを作りたいという方は、是非、ご検討願います。